
XIni = input("Enter initial guesses (Must be a column vector: \n") Įrror("Partial Pivoting does not make the coefficient matrix a diagonally dominant matrix.")ĭisp("Partial Pivoting makes the coefficient matrix a diagonally dominant matrix. ShowSteps = false %true shows calculation stepsĪ = input( 'Please Enter the Co-efficient Matrix, A:\n' ) ī = input( 'Please Enter the Constants(Must be a column vector, b:\n')

I wasn't sure if this would have been more appropriate on stack overflow, but I think my actual problem is with my math, which is why I posted it here.%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Title: Gauss Seidel method % % Author: Dhiman Roy, Dept.

What equation should I use for my Gauss-Seidel program, or what can I fix in my current equation to get the values provided in the key? Because I'm getting a different value, I think there must be some error in my equation. Returns, which is different in the last decimal place than the key showsįrom what I understand, my equation should work, as according to the Gauss-Seidel method, I'm using the new value of x and y for the iterations. To test your function, note that gs1_method(2) should return the list (x 0, y 0) = (0, 0) as your starting approximation. Negative integer n, and returns a list, where x_n and y_n are the values of x_n and y_n respectively for the Gauss-Seidel method when applied to system (1) above. Returns ĭefine a function, called gs1_method, which accepts as input a single non. Consider again the linear equations in (). So I know I have this first iteration right as Previous: The Jacobi Method Up: Stationary Iterative Methods Next: The Successive Overrelaxation Method Previous Page: Convergence of the Jacobi method Next Page: The Successive Overrelaxation Method The Gauss-Seidel Method. To test your function, note that gs1_iteration(3,5) should return Ever heard of the Jacobi Method Well, the Gauss-Seidel is nothing but a better version of the Jacobi. Gauss-Seidel (also known as successive displacement method) is a mathematical computational method mainly used to find the solution of a System of Linear Algebra.
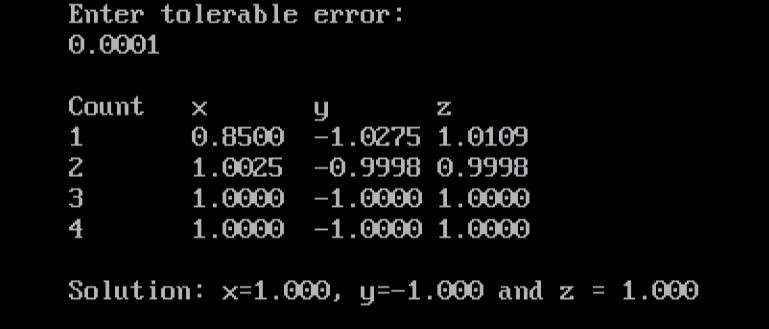
In other words, gs1_iteration(x,y) should return the results of performing one iteration of the Gauss-Seidel method for system (1) on the inputs x, y. Implementing Gauss Seidel Method in Java. Using the Gauss-Seidel method and equations (2) and (3). , where new_x is the updated value x_n and new_y is the updated value y_n X and y (which we think of as being x n-1 and y n-1 respectively), and returns a list Define a function, called gs1_iteration, which accepts as input values for


 0 kommentar(er)
0 kommentar(er)
